توابع هیپربولیک
تعریف
سینوس هیپربولیک :
کسینوس هیپربولیک :
تانژانت هیپربولیک :
کتانژانت هیپربولیک :
سکانت هیپربولیک :
کسکانت هیپربولیک :

آموزش توابع هیپربولیک
سینوس هیپربولیک و کسینوس هیپربولیک با قواعدی به هم مربوط می شوند که بسیار شبیه قواعدی هستند که سینوس و کسینوس را به هم ربط می دهند و همان طور که می توان سینوس وکسینوس را با نقطه ی واقع بر دایره ی واحد مشخص کرد، توابع سینوس هیپربولیک و کسینوس هیپربولیک را نیز می توان با مختصات نقطه ای چون واقع بر هذلولی واحد مشخص ساخت چرا که:
شباهت ها و تفاوت های توابع هیپربولیک وتوابع مثلثاتی
الف) شباهت ها:
- چون
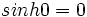 و
و 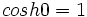 ، همه ی توابع هیپربولیک در صفر همان مقادیری را دارند که توابع مثلثاتی متناظرشان دارند.
، همه ی توابع هیپربولیک در صفر همان مقادیری را دارند که توابع مثلثاتی متناظرشان دارند. - کسینوس هیپربولیک تابعی زوج است و سینوس هیپر بولیک تابعی فرد، بنابر این نمودار
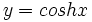 نسبت به محور
نسبت به محور 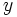 ها و نمودار
ها و نمودار 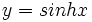 نسبت به مبدا متقارن است. پس در این مورد هم توابع هیپربولیک مانند نظایر مثلثاتی شان عمل می کنند.
نسبت به مبدا متقارن است. پس در این مورد هم توابع هیپربولیک مانند نظایر مثلثاتی شان عمل می کنند.
سلام خانم
ممنون از این مبحثتون
من واقعا با توابع هیپربولیک درگیرم!!
در این سطحی که شما دارید مطرح میکنید ،مشکلی ندارم.اما در سطوح بالاتری نظیر استفاده از این توابع در انتگرالهای دوطرفه یا بعضی از اثباتهای حد توابع چند متغیره واقعا به مشکل برمیخورم.
اقتصاد هم که تا دلتون بخواد توش انتگرال های دو طرفه است.
میخواستم خواهش کنم که اگر مقدوره مطالب رو به سطح پیشرفته نزدیک کنید.
معکوس توابع هیپربولیک
برهان وجودی
چون 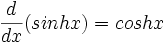 به ازای هر مقدار
به ازای هر مقدار  مثبت است، تابع سینوس هیپربولیک تابعی صعودی بر حسب
مثبت است، تابع سینوس هیپربولیک تابعی صعودی بر حسب  بوده و بنابر این معکوسی دارد که آن را به صورت
بوده و بنابر این معکوسی دارد که آن را به صورت 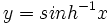 نمایش می دهند. به ازای هر مقدار
نمایش می دهند. به ازای هر مقدار  در بازه ی
در بازه ی 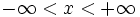 ، مقدار
، مقدار 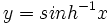 عددی است که سینوس هیپربولیک آن صفر است. نمودارهای
عددی است که سینوس هیپربولیک آن صفر است. نمودارهای 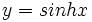 و
و 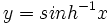 در شکل1 آمده اند.
در شکل1 آمده اند.
هیپربولیک
تابع 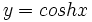 ، همان طور که در شکل2 نمایش داده شده است، یک به یک نیست. ولی تابع محدود شده ی
، همان طور که در شکل2 نمایش داده شده است، یک به یک نیست. ولی تابع محدود شده ی 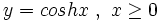 یک به یک بوده و بنابراین دارای تابع معکوس است. این معکوس را به صورت
یک به یک بوده و بنابراین دارای تابع معکوس است. این معکوس را به صورت 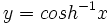 نشان می دهند. به ازای هر مقدار
نشان می دهند. به ازای هر مقدار 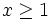 ،
، 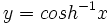 عددی در بازه ی
عددی در بازه ی 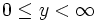 است که کسینوس هیپربولیک آن،
است که کسینوس هیپربولیک آن،  است.
است.
اگر سئوالی در ارتباط با توابع هیپربولیک و هذلولی دارید ، اینجا مطرح کنید.

